作者:聚创暨大考研网-a老师
点击量: 758
发布时间: 2016-08-22 16:23
【微信号:扫码加咨询】

暨南大学2017年考研大纲已公布,以下是聚英考研网为大家整理的2017年暨南大学硕士研究生入学考试819材料力学考试大纲,具体内容如下:
暨南大学力学与土木工程系硕士研究生入学考试
《材料力学》考试大纲
目录
I. 考察目标
II. 考试形式和试卷结构
III. 考察范围
IV. 试题示例
V.参考资料
I. 考察目标
材料力学考试内容涵盖杆件在四种基本变形(拉压、剪切、弯曲、扭转)下的强度和刚度计算,应力分析和强度理论、组合变形、压杆稳定。要求考生对材料力学中的基本概念、假设和结论有正确的理解,基本了解材料力学应用的工程背景,具有将一般构件简化为力学简图的分析能力。熟练掌握处理杆类构件或零件强度,刚度及稳定性等力学问题的基本方法,具有比较熟练的计算能力与设计能力。
II. 考试形式和试卷结构
一、试卷满分及考试时间
本试卷满分为150分,考试时间为180分钟。
二、答题方式
闭卷,笔试。
三、试卷内容结构
轴向拉压变形 20分
剪切变形 5分
扭转变形 15分
弯曲变形 30
组合变形 15分
应力分析和强度理论 20分
压杆稳定 10分
能量法 15
超静定结构 20
四、试卷结构
单项选择题10分(5小题,每题2分)
填空题10分(每题2分)
简答题40分
综合应用题90分
III. 考察范围
轴向拉伸与压缩
[考察目标]
掌握轴向拉伸与压缩的概念,轴向拉压杆件的内力和应力计算。了解金属材料拉伸和压缩时的力学性能,安全系数与许用应力。熟练掌握拉压杆件的强度计算,及轴向拉伸与压缩时杆件的纵向变形、线应变、横向变形计算。掌握简单拉 ( 压 ) 超静定问题的一般解法。了解应力集中概念。
[考察范围]
一、轴向拉伸与压缩的概念、直杆横截面上的内力和应力计算。
二、斜截面上的应力情况。
三、金属(低碳钢与铸铁)材料拉伸和压缩时的力学性能。
四、失效和安全系数,拉压杆件的强度计算。
五、轴向拉伸与压缩时杆件的纵向变形、横向变形计算,结构节点位移的计算。
剪 切
[考察目标]
理解剪切和挤压概念;掌握剪切和挤压的实用计算。
[考察范围]
一、剪切和挤压概念。
二、连接件的强度校核。
扭 转
[考察目标]
理解扭转、纯剪切、切应变、切应力互等定理、剪切虎克定律、极惯性矩和抗扭截面模量的概念。掌握扭矩的计算和扭矩图的作法。掌握圆轴扭转应力与扭转变形分析,圆轴的强度与刚度计算。
[考察范围]
一、扭转的概念,功率、转速和外力偶的关系。扭矩的计算和扭矩图的作法。
二、纯剪切、切应变、切应力互等定理、剪切虎克定律。
三、圆轴扭转应力的计算。圆轴的强度计算。
四、圆轴扭转变形分析与刚度计算。
弯曲内力
[考察目标]
理解对称弯曲、剪力和弯矩的概念。了解静定梁的基本形式。掌握梁的剪力和弯矩方程的求法。掌握梁的剪力图和弯矩图、刚架内力图的作法。掌握剪力、弯矩和分布载荷集度的微分关系及其应用。了解平面刚架和曲杆的弯曲内力。
[考察范围]
一、对称弯曲的概念,静定梁的分类。
二、剪力方程和弯矩方程。
三、用分布荷截、剪力、弯矩的关系作内力图。
四、平面刚架和曲杆的内力图。
弯曲应力
[考察目标]
掌握纯弯曲梁的正应力公式,弯矩和挠度曲线曲率半径的关系。理解抗弯截面模量,抗弯刚度的概念。了解梁弯曲切应力的分布。了解非对称截面梁平面弯曲的条件。掌握梁的强度计算。理解提高弯曲强度的措施。
[考察范围]
一、纯弯曲梁的正应力公式的推导。
二、横力弯曲梁的正应力强度计算。
三、梁的切应力强度计算。
四、提高梁承载能力的措施。
弯曲变形
[考察目标]
掌握挠度和转角的概念,挠曲线的近似微分方程。掌握积分法、叠加法计算梁的挠度和转角。了解提高梁刚度的措施。
[考察范围]
一、梁截面的挠度和转角的概念,梁挠曲线近似微分方程。
二、用积分法求梁的变形。
三、叠加法求梁的变形。
四、梁的刚度校核,提高梁弯曲刚度措施。
应力状态和强度理论
[考察目标]
理解应力状态,主应力和主平面的概念。掌握平面应力状态分析的解析法、图解法。掌握三向应力圆的作法。理解最大切应力,广义虎克定律,体积应变,弹性比能,体积改变能密度和畸变能密度。理解强度理论的概念,掌握材料破坏形式分析,掌握第一、二、三、四强度理论的观点、强度条件及其适用范围。了解莫尔强度理论。
[考察范围]
一、应力状态的概念。
二、平面应力的应力状态分析:数解法、图解法。
三、应力状态分类,空间应力分析,一点的最大应力。
四、广义虎克定律,复杂应力状态的应变能密度。
五、强度理论的概念,材料的两种破坏形式。
六、第一、二、三、四强度理论及其应用。
组合变形
[考察目标]
理解组合变形的概念与实例。掌握拉(或压)弯组合变形、两个相互垂直平面的弯曲、弯扭组合变形的应力与强度计算。
[考察范围]
一、拉伸(压缩)与弯曲的组合。
二、两个相互垂直平面的弯曲。
三、扭转与弯曲的组合。
压杆稳定
[考察目标]
理解压杆弹性平衡稳定性的概念。掌握细长压杆的临界载荷-欧拉公式、超过比例极限时压杆的临界力—经验公式,了解临界应力总图。掌握压杆稳定性设计的步骤,理解提高压杆稳定性的措施。
[考察范围]
一、压杆稳定的概念。
二、细长压杆临界力的欧拉公式。
三、欧拉公式的适用范围,临界应力总图。
四、压杆稳定的实用计算。
五、提高压杆稳定的措施。
能量法
[考察目标]
理解能量法,功、位移互等定理等概念。掌握杆件变形能的计算。掌握卡氏第二定理、单位载荷法(莫尔积分)。
[考察范围]
一、外力功与杆件应变能的计算,余能的概念及计算。
二、卡氏第一定理、余能定理、卡氏第二定理。
三、运用卡氏第二定理求解结构超静定问题。
四、单位荷载法(莫尔积分)。
超静定问题
[考察目标]
掌握简单拉压、扭转以及弯曲超静定问题的求解方法。掌握力法求解超静定结构,能利用对称及反对称性质来简化超静定结构的求解。
[考察范围]
一、超静定结构的有关概念。
二、拉压简单超静定问题。
三、扭转简单超静定问题。
四、简单超静定梁。
五、用力法求解超静定结构,并利用结构对称及反对称性质。
附录A 平面图形的几何性质
[考察目标]
熟练计算静矩,惯性矩和惯性积,形心主轴和主形心惯性矩。掌握平行移轴公式及转轴公式。
[考察范围]
一、平面图形的静矩、形心位置、惯性矩、极惯性矩、惯性积的概念。
二、平行移轴定理。
三、形心主惯性轴、形心主惯性矩的概念及计算。
IV. 试题示例
一、单选题(共5小题,每小题2分,共10分)
试题示例:
1. 从力学的角度出发,构件要安全可靠工作必须满足三方面的要求。以下哪个不属于这些要求?( )
A. 强度要求 B. 小变形要求 C. 刚度要求 D. 稳定性要求
2. 关于材料拉伸时的力学性能,说法不正确的是( )
A. 低碳钢拉伸破坏前经历了弹性阶段、屈服阶段、强化阶段、局部变形阶段;
B. 铸铁拉伸破坏时没有发生明显的塑性变形;
C. 屈服现象的特点是应变基本保持不变,而应力显著增加;
D. 在强化阶段卸载后重新加载,低碳钢的比例极限会提高。
3. 材料力学主要研究哪一类工程构件?( )
A. 块体 B. 板 C. 壳 D. 杆件
4. 对于受剪切杆件的强度计算问题,说法正确的是( )
A. 仅需考虑剪切实用计算;
B. 仅需考虑挤压强度计算;
C. 既要进行剪切强度计算又要进行挤压强度计算。
5. 关于梁纯弯曲时横截面上的正应力分布规律,说法不正确的是( )
A. 正应力正比于截面对中性轴的惯矩Iz,反比于弯矩M;
B. 正应力随截面高度y呈线性分布;
C. 中性层处的正应力为零;
D. 截面凸出一侧受拉应力,凹入一侧受压应力。
二、填空题(每题2分,共10分)
1. 变形固体的三个基本假设是 。
2. 现有三种材料A、B、C的拉伸曲线如图所示,分别由这三种材料制成同一构件,则:1)强度最高的是 ;2)抗拉刚度最大的是 ;3)塑性最好的是 。

3. 在进行结构强度分析时,通常以应力作为是否满足强度设计要求的指标。应力通常可以分为 和 两类。
4. 已知如图所示结构中三杆的拉压刚度均为EA,设杆AB为刚性体,杆AB长L。则在载荷F作用下,C点的竖向位移为 ,水平位移为 。
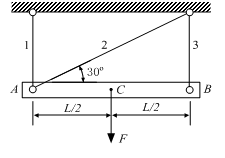
……
三、简答题(共40分)
1. 请列出静定结构与超静定结构的主要区别,并简述用力法求解超静定结构的步骤。
2. 请分别叙述杆件发生每种基本变形时,横截面上有何种内力?其应力如何分布?
3. 请写出四个常用强度理论的强度条件,并说明它们的选用原则。
…….
四、综合应用题(共90分)
1、图示简单桁架,设AB和AC分别为直径是20mm和24mm的圆截面杆,E=200GPa,F=5kN。求A点的垂直位移。
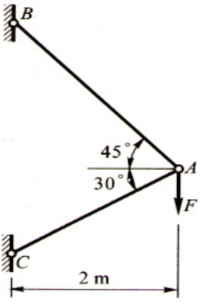
题1图
2、如图所示圆锥形扭杆,A、B两端面直径分别为,两端扭转力偶为,材料的剪切模量为G,试求杆内最大切应力与相对扭转角的表达式。
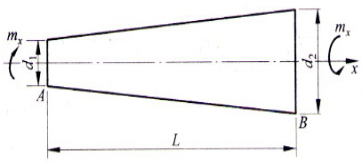
题2图
3、钢制外伸梁受力如图a)所示。截面尺寸如图b)所示(单位:mm)。已知。
1)画出梁的剪力图和弯矩图,要求:求出支座反力,并在图上标出关键点的内力数值;
2)对梁进行正应力强度校核。
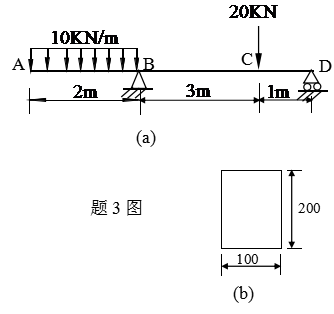
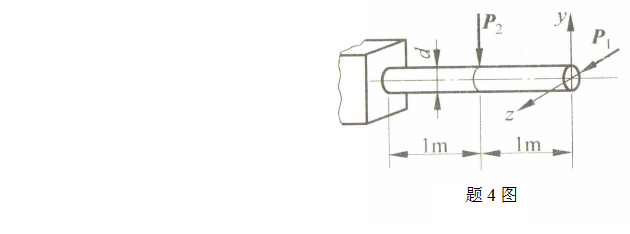
4、图示低碳钢制成的悬臂梁受水平力及铅垂力。梁横截面为圆形,,MPa。试求:1)指出危险点位置并求梁内的最大正应力;2)选用合适的强度理论对梁进行强度校核。
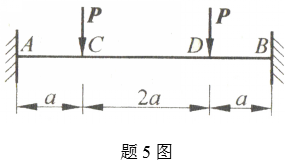
5、两端固支梁受力如图所示。其抗弯刚度为EI,试用力法(正则方程)求约束反力,并绘制出梁的弯矩图。
V.参考资料
[1]孙训方,《材料力学》第四版(I,II),高教出版社,2002年。
[2]刘鸿文,《材料力学》第四版(I,II),高教出版社,2004年。
[3]单辉祖,《材料力学》(I,II),高教出版社,2004年。
[4]顾志荣,吴永生,《材料力学》(上,下),同济大学出版社,1998年。
[5]宋子康,《材料力学》,同济大学出版社,2001年。
以上是聚创考研网为考生整理的"2017年暨南大学硕士研究生入学考试819材料力学考试大纲"的相关考研信息,希望对大家考研备考有所帮助! 备考过程中如有疑问,也可以添加老师微信H17720740258进行咨询。




