作者:聚创考研网-a老师
点击量: 472
发布时间: 2016-11-19 11:38
【微信号:扫码加咨询】

为了方便广大考生复习数学的知识点,聚英考研信息网将考研数学的知识点进行了整合,方便大家学习记忆相关知识点,以下是概率论基础知识之随机事件概念,希望对大家有所帮助,如果大家在前期的考研中有关于规划和常识的疑惑,欢迎随时私撩我们的考研专家杨老师QQ2355951269,为你指点迷津,助你研路~

随机事件的几个概念:
1、随机实验
满足下列三个条件的试验称为随机试验;(1)试验可在相同条件下重复进行;(2)试验的可能结果不止一个,且所有可能结果是已知的;(3)每次试验哪个结果出现是未知的;随机试验以后简称为试验,并常记为E。
例如:E1:掷一骰子,观察出现的总数;E2:上抛硬币两次,观察正反面出现的情况;
E3:观察某电话交换台在某段时间内接到的呼唤次数。
2、随机事件
在试验中可能出现也可能不出现的事情称为随机事件:常记为 A,B,C……
例如,在E1中,A表示“掷出2点”,B表示“掷出偶数点”均为随机事件。
3、必然事件与不可能事件
每次试验必发生的事情称为必然事件,记为Ω。每次试验都不可能发生的事情称为不可能事件,记为Φ。
例如,在E1中,“掷出不大于6点”的事件便是必然事件,而“掷出大于6点”的事件便是不可能事件,以后,随机事件,必然事件和不可能事件统称为事件。
4、基本事件
试验中直接观察到的最简单的结果称为基本事件。
例如,在E1中,“掷出1点”,“掷出2点”,……,“掷出6点”均为此试验的基本事件。
由基本事件构成的事件称为复合事件,例如,在E1中“掷出偶数点”便是复合事件。
5、样本空间
从集合观点看,称构成基本事件的元素为样本点,常记为e.
例如,在E1中,用数字1,2,……,6表示掷出的点数,而由它们分别构成的单点集{1},{2},…{6}便是E1中的基本事件。在E2中,用H表示正面,T表示反面,此试验的样本点有(H,H),(H,T),(T,H),(T,T),其基本事件便是{(H,H)},{(H,T)},{(T,H)},{(T,T)}显然,任何事件均为某些样本点构成的集合。
例如, 在E1中“掷出偶数点”的事件便可表为{2,4,6}。试验中所有样本点构成的集合称为样本空间。记为Ω。
例如,
在E1中,Ω={1,2,3,4,5,6}
在E2中,Ω={(H,H),(H,T),(T,H),(T,T)}
在E3中,Ω={0,1,2,……}
例1、一条新建铁路共10个车站,从它们所有车票中任取一张,观察取得车票的票种。
此试验样本空间所有样本点的个数为NΩ=P 210=90.(排列:和顺序有关,如北京至天津、天津至北京)
若观察的是取得车票的票价,则该试验样本空间中所有样本点的个数为: 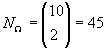 (组合)
(组合)
例2、随机地将15名新生平均分配到三个班级中去,观察15名新生分配的情况。此试验的样本空间所有样本点的个数为: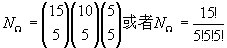
第一种方法用组合+乘法原理;第二种方法用排列。
相关阅读推荐:
以上是聚创考研网为考生整理的"2018考研数学概率论基础知识之随机事件概念"的相关考研信息,希望对大家考研备考有所帮助! 备考过程中如有疑问,也可以添加老师微信H17720740258进行咨询。




